Handbook of experimental
psychology.
Edited by S.S.Stevens.
John Wiley & Sons, Inc., New York Chapman & Hall, Ltd.,
Экспериментальная психология (том 2)
редактор-составитель американского издания - С.С.Стивенс
перевод с английского под редакцией действительного члена Академии медицинских
наук СССР П.К.Анохина и доктора педагогических наук В.А.Артёмова
Издательство иностранной литературы, Москва, 1963
XXV. Основные корреляты слухового стимула
Дж. К.
Р. Ликлайдер
(Массачусетский
технологический институт)
При изучении слуха так
же, как и в других областях психологии, основным является раскрытие природы
стимула. Поэтому в начале данной главы мы рассмотрим некоторые основные
характеристики звуковых колебаний и одновременно установим терминологию,
наиболее точно определяющую эти характеристики.
Формы
колебаний звуковых волн
При колебании мембраны
репродуктора происходит попеременное сгущение и разрежение воздуха.
Образовавшееся при сжатии давление в непосредственно прилегающем к мембране
слое воздуха передается к более удаленным от мембраны слоям воздуха; таким
образом осуществляется распространение волны. При этом сами частицы воздуха
незначительно удаляются от своего первоначального положения, зато звуковая
волна, то есть сгущение и разрежение, распространяется быстро и на большое расстояние.
При обычной температуре скорость распространения звука в воздухе составляет
несколько более 1100 фут/сек (от 330 до 340 м/сек). Действуя на барабанную
перепонку, эти звуковые волны становятся слуховым стимулом. Звуковые волны
можно записать при помощи микрофона, снабженного зондом в виде узкой трубки,
конец которой можно поместить на расстоянии 1 мм от барабанной перепонки.
Рассматривая изменяющееся звуковое давление как функцию времени, мы можем
получить представление об акустическом стимуле, который будет определен как звуковое
давление у барабанной перепонки.
Запись изменения
давления непосредственно у самой барабанной перепонки имеет то преимущество,
что дает возможность получить значения, наиболее близкие к тем, которые
предполагаются в слуховом рецепторе, хотя такой метод и представляет серьезные
затруднения. Во-первых, трудность заключается в сложности измерения. Во-вторых,
мы не располагаем микрофонами, обеспечивающими точное воспроизведение сложных
звуковых волн. В-третьих, получаемые результаты подобных измерений до некоторой
степени зависят от свойств барабанной перепонки.
Возможен и другой
метод определения звукового давления как функции времени, при котором
достигается независимость измерений от характеристик человеческого уха:
измерения могут производиться в свободном звуковом поле, то есть в безэховом
(свободном от эха) пространстве, как показано на фиг. 1. Звуковое давление
измеряется в точке, соответствующей тому положению, в котором находился или
будет находиться центр головы испытуемого. Результирующий график давления как
функции времени представляет собой звуковое давление в свободном поле.
Хотя объектом обычных измерений является звуковое давление, последнее отнюдь не
является единственным аспектом звукового колебания.
Подобным же образом
можно нанести на графике сдвиг частиц воздуха как функцию времени от их
первоначального положения (смещение частиц) или скорость их колебательного
движения (колебательная скорость). Но самое примечательное заключается в том,
что если нам известны свойства среды, то данные всех трех величин будут
одинаковы. В свободном поле звуковое давление и колебательная скорость в
продольном колебании по форме идентичны, а смещение частиц является временным
интегралом любой из двух других величин.

Фиг. 1. Безэховая
камера для исследования акустики и слуха. Клиновидные пальцы, выступающие из
пола, потолка и стен, изготовлены из фибростекла, покрытого миткалем.
При приближении к
границам камеры звуковые волны улавливаются волокнистой паутиноподобной
структурой клиньев. Эффект отражения настолько мал,что явлением эха и наличием
стоячих волн в данных условиях можно пренебречь. Камера обеспечивает условия
свободного поля, которые необходимы при большинстве основных измерений в
области психоакустики (по Беранеку, Слиперу и Мутсу, 1945).
Форма волны - это
временное представление акустического сигнала. Оно имеет два измерения: время и
амплитуду (причем этот термин будет общим для давления, скорости и смещения).
Этих данных вполне достаточно для определения отношения стимула к слуху
(монауральному). Тем не менее временное представление не единственный способ,
при помощи которого можно выразить данное соотношение.
Спектр
Другой метод,
основанный на частотном представлении, был разработан на базе установленного
Фурье (1822) положения, согласно которому колебание любой формы может быть
разложено в ряд синусоидальных колебаний или синтезировано из них. Учитывая
это, следует отнестись с должным вниманием к свойствам синусоидальных
колебаний.
Слово
"синусоидальный" обозначает тип простых гармонических колебаний, то
есть наиболее элементарных колебаний, из которых чаще всего встречается
синусоида А (фиг. 2). Любую синусоиду можно определить тремя характеристиками:
частотой, максимальной амплитудой */Максимальная амплитуда (амплитуда)
обозначается буквой А в отличие от меняющейся мгновенно амплитуды, обозначаемой
через а./ и фазовым углом.
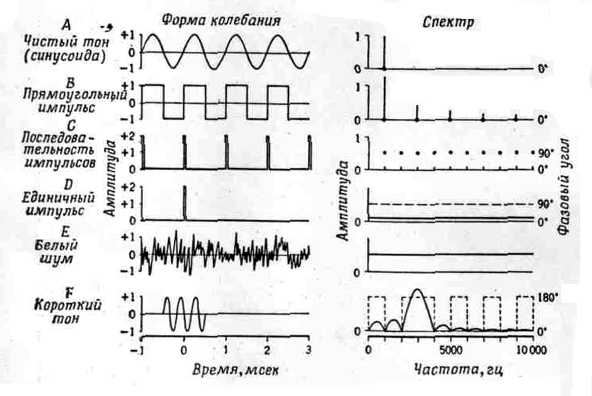
Ф и г. 2. Колебания
и спектры. В каждой из шести пар графиков колебания (слева), показывающие
амплитуду как функцию времени, дают такие же дан-ные, как и спектр (справа),
показывающий амплитуду и фазовый угол как функции частоты.
Графики колебаний должны пониматься как имеющие бесконечное продолжение в
обоих направлениях. Графики спектра предполагают бесконечное продолжение
вправо. Амплитуда (жирные линии) определяется в произвольных единицах, а
фазовый угол (пунктирные линии или крупные точки) в градусах.
Частота - это число
колебаний в единицу времени, то есть количество периодов в 1 сек (герцы).
Амплитуда представляет собой максимальное смещение от нулевого положения.
Фазовый угол, имеющий значение только по отношению к произвольно выбранному
исходному моменту, определяет участок периода, на котором находится точка,
соответствующая исходному моменту */В выражении a=A sin (2pft+j) вся величина 2pft+j
представляет собой мгновенный фазовый угол. Он содержит постоянный член j,
который мы определяем как третий параметр синусоиды/.
Для того чтобы иметь
удобный метод определения фазы, делим полный период на 360°, или 2p радиан,
начиная от оси ординат.
Если начало периода
(0°) совпадает со временем t=0, как это показано на фиг. 2.А, мы рассматриваем
это колебание как синусоидальную волну. Если t=0 соответствует максимуму
звуковой волны (фазовый угол равен 90°), мы рассматриваем данную волну как
косинусоидальную. Если ни одно из этих положений не имеет места, мы определяем
начальную фазу при t=0 в градусах или радианах.
Цель частотного
анализа состоит в том, чтобы разложить сложную волну на синусоидальные
составляющие различной частоты, а затем представить ее в виде максимальных
амплитуд и фаз частотных составляющих. Данный процесс показан на фиг. 3.
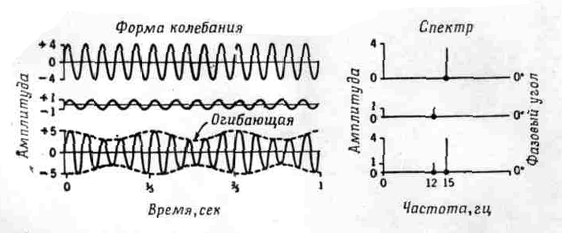
Фиг. 3. Пример
перехода от колебаний к спектру.
Сложное колебание,
заключенное между двумя огибающими, обозначенными пунктиром, образовано путем
сложения ординат двух синусоид, помещенных выше.
Чтобы произвести
частотный анализ, мы, следовательно, раскладываем сложное колебание на
составляющие (для этой цели разработаны фотоэлектрические и механические
анализаторы, а также методы математического анализа).
Для каждой
составляющей мы определяем частоту, максимальную амплитуду и фазовый угол при
t=0. Спектральное представление сложного колебания осуществляется
последовательным расположением спектров простых колебаний так, как это показано
в нижнем правом углу фиг. 3.
Вертикальные линии на
шкале частот расположены в точках, соответствующих 12 и 15 гц, так как первое
значение содержит 12 полных периодов в 1 сек, а второе - 15.
Высота линий
определяет максимальную величину амплитуд синусоидальных составляющих, а то
обстоятельство, что две точки помещаются на нулевой линии рядом, показывает,
что две составляющие являются синусоидальным колебанием (нулевой фазовый угол
при времени t=0).
Зависимость
между формой колебания и спектром
Спектр в его трех параметрах
(частота, максимальная амплитуда и фаза) характеризует звуковую волну полностью
и однозначно, подобно колебанию в его двух измерениях (амплитуда и время). Тем
не менее в каждом конкретном случае тот или другой из указанных видов описания
звуковой волны окажется более подходящим для данной цели.
Следовательно,
представление колебания в виде спектра и спектра как колебания, называемое
преобразованием Фурье, является важным средством изучения слуха. В пределах
данной главы мы не имеем возможности вдаваться в подробности математического
анализа, а поэтому изучение параллельных графиков, показанных на фиг. 2,
поможет полнее охватить интересующую нас проблему.
Мы уже рассмотрели
синусоидальную волну A с ее периодическими колебаниями и однокомпонентным спектром.
Установлено, что колебание прямоугольной формы в качестве одной из своих
составляющих имеет синусоиду той же частоты и фазы, как и волна A, но с
несколько большей величиной максимальной амплитуды. Кроме того, к этой основной
составляющей (первой гармонике) добавляется ряд гармоник более высокого тона -
синусоид с частотами, кратными основной частоте.
Следует отметить, что
в данном случае множители представляют собой целые нечетные числа: 1000 гц,
1000 гц умноженные на 3, умноженные на 5 и т. д. Кроме того, гармоники
представляют собой синусоидальные колебания (фазовый угол равен 0°), и их
максимальные амплитуды обратно пропорциональны их частотам. Для точного
графического изображения диапазона спектра колебаний прямоугольной формы
пришлось бы продолжать график бесконечно далеко вправо, так как, хотя
высокочастотные составляющие и очень слабы, в идеально прямоугольном импульсе
будут присутствовать все нечетные гармоники. Колебания идеально прямоугольной
формы в природе не встречаются, так как частицы воздуха имеют конечную массу и,
следовательно, им нельзя сообщить бесконечно большое ускорение, которое следует
из прямоугольной формы волны.
Интересно сравнить ряд
импульсов (см. фиг. 2.С), имеющих прямоугольную форму с единичным импульсом.
Ряд импульсов имеет
как четные, так и нечетные гармоники. Компоненты представляют собой вместо
синусоид косинусоиды (фазовый угол равен 90°), и в качестве первой
аппроксимации - все представленные на фиг. 2 гармоники одинаково сильны или,
что более удобно, одинаково слабы. Наличие четных гармоник в спектре импульса
объясняется тем, что колебание происходит не около центральной оси, как в
случае волны прямоугольной формы; наличие косинусоидальных компонентов вместо
синусоидальных объясняется тем, что колебание располагается симметрично по
отношению к вертикальной линии, когда t=0.
Однородность спектра
импульсов объясняется краткостью самих импульсов. Путем создания достаточно
коротких колебаний степень однородности спектра может быть распространена до
любой желаемой частоты.
Если имеется только
один импульс (см. фиг. 2.D), то спектр все же остается однородным. Однако в
этом случае энергия не концентрируется на определенных частотах, а
распределяется по всей шкале частот. Данное явление носит название сплошного
спектра, тогда как спектры синусоидального колебания и колебания прямоугольной
формы являются линейчатыми спектрами. Шкала максимальной амплитуды спектра
единичного импульса не калибрована, и ввиду того, что энергия единичного
импульса распределяется среди бесконечно большого числа частотных составляющих,
величина максимальной амплитуды каждой составляющей будет беско-нечно малой.
Тем не менее шкала фазового угла может быть размечена, как раньше; все
составляющие представляют собой косинусоидальные колебания.
Белый шум, как его
часто называют (см. фиг. 2.E), или шум, созданный беспорядочными колебаниями,
представляет особый интерес, поскольку он присутствует всегда. Вследствие
термического движения молекул воздуха создается шум, который только на
незначительную величину слабее слышимого. Колебания электронов в проводниках и
вакуумных лампах создают шум, подобный "шипению" в радиоприемниках и
репродукторах. Распределение мгновенных значений амплитуд следует кривой
нормального распределения. Спектр однороден по максимальной амплитуде и случаен
по фазе.
Одним из путей
определения зависимости между колебанием и спектром может явиться способ
наложения бесконечно большого числа волн с различными частотами. Поскольку
фазовые отношения между синусоидами точно не установлены, последние либо
усиливают, либо ослабляют друг друга в совершенно случайном порядке.
В заключение несколько
слов о коротком тоне (см. фиг. 2.F). Одной из причин, вследствие которых
короткие тона имеют практическое значение в исследованиях слуха, является та,
что в реальном эксперименте мы не можем представить слухового стимула в
бесконечности, которая была бы необходима для создания идеально чистого тона.
При включении или выключении тона чистота последнего нарушается. Всякий раз,
когда мы изменяем частоту, максимальную амплитуду или фазу тона, мы
распределяем его энергию по всей частотной шкале. Примером этого является
спектр, показанный на фиг. 2.F. Вместо энергии, сконцентрированной на частоте
3000 гц, как можно было ожидать, зная, что в 1 мсек укладывается три периода,
мы находим почти непрерывное распределение энергии начиная с 0 до 10 000 гц.
Следует признать, что это крайний случай; для более длительных тонов энергия
спектра концентрируется более тесно близ центральной частоты. Но основное
положение остается неизменным: как тольком мы меняем что-либо, связанное с
чистым тоном, чистота его утрачивается.
Энергетический
спектр и автокорреляционная функция
Как мы видели, спектр
белого шума в пределах рассматриваемого частотного диапазона содержит
одинаковое (бесконечно малое) количество энергии на каждой частоте, но фазовые
углы компонентных синусоид распределяются случайно. Поэтому при рассмотрении
сигналов, подобных белому шуму, мы можем изучать их в таком представлении,
которое бы не несло никакой информации о фазах. Это достигается путем введения
среднеквадратичной амплитуды вместо максимальной амплитуды и фазы каждого из
компонентов. Поскольку в среде, оказывающей сопротивление, энергия
пропорциональна квадрату амплитуды, то соотнесение значения средней квадратичной
амплитуды к частоте называется энергетическим спектром. Следует отметить, что
вследствие однородности спектра белого шума в пределах, показанных на фиг. 2.E,
замена максимальной амплитудой составляющих среднеквадратичной амплитуды меняет
картину только в той степени, что масштаб по оси ординат должен быть изменен.
Другой путь выражения
информации содержащейся в энергетическом спектре, заключается в определении
функции автокорреляции колебания. Автокорреляционная функция находится путем
двукратного изображения одного и того же колебания (причем второе изображение
вычерчивается под первым) и определения корреляции между соответствующими
ординатами двух кривых. Если вторая кривая расположена непосредственно под
первой, то корреляция представляет собой единицу. Если же вторая кривая
сдвинута во времени по отношению к первой на величину t, то корреляция в общем
становится меньше единицы. Величина корреляции между исход-ной и сдвинутой
волнами, соотнесенная со значением сдвига t, дает нам полезную картину сигнала.
Полученное соотношение r (коэффициента корреляции) и t (сдвига) представляет
собой нормализованную автокорреляционную функцию. Нормализованной она
называется для того, чтобы отличить ее от другой тесно связанной с ней
функцией, определяющей отношение среднеквадратичной величины произведения
исходной и сдвинутой волн к величине сдвига. Последняя, называемая
ненормализованной автокорреляционной функцией, равняется первой, умноженной на
среднеквадратичную ординату исходной волны, и представляет собой преобразование
Фурье энергетического спектра. Таким образом, она имеет такое же отношение к
энергетическому спектру, какое звуковая волна имеет к спектру, определяющему
максимальную амплитуду и фазу.
На фиг. 2.Е мы видим,
например, что колебание изменяется вверх и вниз настолько быстро, что
корреляция между волной, сдвинутой при своем продолжении даже на незначительную
величину, несомненно сведется к нулю, так как между амплитудой в какой-либо
определенный момент и амплитудой в точке, несколько отставленной по времени,
практически нет никакого различия. Не будет никакого различия также и в случае
идеально случайного шума с его однородным энергетическим спектром, однообразным
до бесконечно высоких частот. Это означает, что полученное для колебания,
изображенного на фиг. 2.E, значение автокорреляционной функции упадет с единицы
(для нулевого сдвига) до нуля (для каждого сколько-нибудь заметного сдвига).
Поэтому функция автокорреляции для белого шума будет иметь приблизительно такую
же форму, какую имеет колебание, показайное на фиг. 2.D. Для проверки того
правила, что энергетический спектр представляет собой преобразование Фурье
функции автокорреляции, можно сравнить спектр, изображенный на фиг. 2.D (представляющий
преобразование Фурье колебания), и тем самым сравнить также преобразование
Фурье функции автокорреляции колебания 2.E со спектром 2.E. Находим, что оба
они представляют собой горизонтальные линии. Поскольку шкалы ординат обоих
графиков произвольны, то две горизонтальные линии функционально идентичны.
Следовательно, правило проверено. Автокорреляционные методы находят все более
широкое применение в различных областях, в частности в области связи.
Всестороннее рассмотрение этих областей применения можно найти в работе Винера
(1949г).
Скачки
и импульсы как основные колебания
Кроме метода
представления сложных колебаний как суммы ряда элементарных синусоидальных
компонентов, имеются и другие методы, согласно которым эти компоненты
несинусоидальны. В 1880г. Хэвисайд разработал метод анализа характеристик линий
связи и кабелей с переменными тестовыми сигналами вместо постоянных.
Используемое им основное колебание представляло собой единственный крутой
скачок амплитуды, подобный подъему или спаду прямоугольного импульса. Любую
сложную волну можно рассматривать как результат наложения ряда таких
ступенчатых волн, поскольку любая кривая может быть как угодно точно
аппроксимирована ступенчатой моделью. Изучая математическую основу метода
Хэвисайда, Карсон (1920) показал, что она хорошо соотносится со способом
представления математических функций, развитых Лапласом. Согласно вычислениям
Лапласа, начальное колебание представляет собой импульс (см. фиг. 2,D),
длительностью которого можно пренебречь, но с амплитудой, достаточной для того,
чтобы площадь под кривой была равна единице. Ввиду большой роли в
экспериментальных исчислениях, связанных с методами Хэвисайда и Лапласа,
акустические стимулы, состоящие из скачков и импульсов, представляют интерес в
опытах по изучению слуха.
Изображение
в координатах интенсивность - частота - время
Как мы видели,
колебание относится к определенным моментам времени, и оно не дает никаких
сведений о частоте; спектр, в свою очередь, рассматривает определенные точки на
шкале частот, но без указания на какие-либо различия между данными, полученными
в различные моменты времени. Хотя временной и частотный анализы обеспечили
основу для создания науки о коммуникации, но ни один из методов не обеспечивает
точного соотношения с действительным поведением любой физической анализирующей
системы.
Ни одна физическая
система не может выделить и зарегистрировать показатели математического
момента. Ни от одной физической системы нельзя получить бесконечность,
необходимую для выделения математической синусоиды. То, что мы хотели бы иметь
при изучении слуха, представляет собой компромиссный метод анализа, который
позволяет выражать звуки такими, какими мы их слышим. Такой метод должен до
некоторой степени обеспечить возможность различения сигналов, следующих друг за
другом во времени (так, например, когда следуют звуки один за другим в слуховой
практике человека), а также определить разницу между сигналами, различающимися
по частоте (звуки с частотой 1000 гц совершенно иные, чем с частотой 2000 гц).
Музыкальная нотная
запись является, конечно, как раз таким методом описания звука с учетом частоты
и времени. Она, правда, скорее применима в искусстве, чем в научных
исследованиях, поскольку многое в этом методе вносится воображением
интерпретатора. Для описания слуховых стимулов нам нужна такая запись, которая
позволила бы не в очень громоздком виде регистрировать всю относящуюся к ним
информацию. Мы можем представить себе, как решить данную задачу, рассмотрев
простую модель.
Изображенная на фиг. 4
слева стойка имеет ряд тяжелых пружин. Все пружины имеют равную упругость, и их
постоянные затухания равны. Так как в нижней части этого ряда вес пружин больше
веса пружин в верхней части, то при ударе верхние пружины колеблются быстрее,
чем нижние. На схеме указана собственная частота каждого настроенного
вибратора. Теперь допустим, что все пружины получают совершенно одинаковые
удары при t = 0 на шкале времени (в нижней части схемы). Небольшая схема А
справа иллюстирует то, что мы называем звуковым давлением при ударе; это просто
короткий импульс. На схеме B показан его спектр (ср. фиг, 2,E).
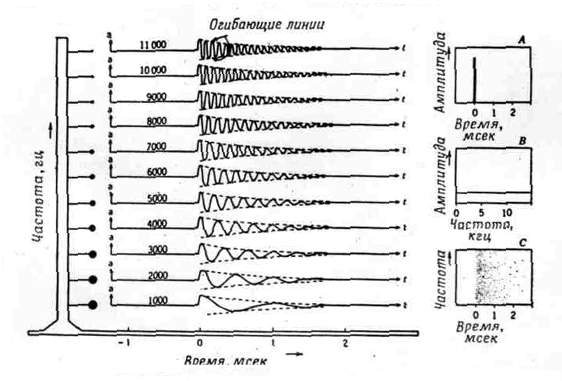
Фиг. 4. Изображение
в координатах интенсивность - частота - время.
Стойка, расположенная налево, имеет ряд резонаторов (пружин) с равным
затуханием, настроенных на указанные частоты. Одновременно все резонаторы
возбуждаются коротким ударом, изображение которого в координатах амплитуда -
время показано на верхней схеме А, а спектр показан на схеме В. Колебательный
характер отклика резонаторов на удар показан в координатах скорость - время (а
по отношению к г) в центре рисунка. Огибающие линии дают наглядную картину
исходного сигнала как такового, то есть импульсного удара. Схема С представляет
собой своеобразный компромисс между А к В. Она показывает аппроксимированно
время удара и равномерное распределение энергии по шкале частот.
Возникает вопрос, как
реагируют на удар подвешенные пружины? Этот вопрос представляет интерес потому,
что мы имеем здесь физическую модель, которая не может дать ни точного анализа
времени, ни точного анализа частоты. Поведение пружины может только дать
возможность представить суть компромиссного метода исследования импульса. В
средней части схемы колебания 11 пружин изображены в виде волн. Окончательное
затухание колебаний каждой пружины происходит при величине максимальной
амплитуды, равной 1/2,718 (1/e), за время, равное 1 мcек, когда величина
амплитуды настолько мала, что ею можно пренебречь. Пунктирными кривыми показаны
огибающие линии. Если ориентироваться только на эти огибающие, мы упустим из
виду некоторые детали, получив наглядное представлениею величине возмущения, но
это значительно упростит изображение. Из данной схемы легко понять, что при
любой частоте, наблюдается одинаковая картина (для каждой подвешенной пружины).
Теперь представим, что у нас имеется не 11, а бесконечно большое количество
пружин, так подобранных, что после равного возбуждения их колебание затухает с
равной скоростью, и так расположенных, что их собственные частоты образуют
частотную шкалу. Вправо от шкалы частот отложим шкалу времени, как показано на
схеме С (см. правую часть фиг. 4). Теперь дадим импульс на бесконечно большое
количество резонаторов и нанесем амплитуды огибающих полученных колебаний
большим или меньшим количеством точек на шкале время - частота. Это даст нам
изображение в трех измерениях: интенсивность (амплитуда огибающих), частота и
время. Данное изображение воспроизводит импульс так же точно, как колебание или
спектр. В данном случае, когда мы обращаем все внимание на огибающие линии, мы
упускаем некоторые детали вследствие пренебрежения фазами колебаний.
Один и тот же метод
анализа может применяться к любому колебанию на входе, а использование
результирующего изображения (схема С) обеспечивает удобную запись сигнала. Этот
метод лег в основу конструкции звукового спектрографа, созданного лабораториями
фирмы "Белл телефон" (Кениг, Данн иЛэйси, 1946), который производит
запись "видимой речи" (ср. гл. XXVI). Конечно, вместо пружин в
звуковом спектрографе используются электрические резонаторы, но главное в этом
методе анализа то, что он дает возможность одновременного исследования того,
что происходит во времени и на определенных частотах.
Если бы представилась
возможность найти подходящий метод записи не только амплитуд огибающих линий, а
самих колебаний в большом количестве резонаторов, мы бы имели еще более
универсальную и гибкую систему (Гэйбер, 1946), которая при известных допущениях
могла бы служить для определения спектра, а при другого рода допущениях - для
определения колебаний. Представим, например, что резонаторы, показанные на фиг.
4, полностью свободны от трения и, следовательно, возникшее колебание никогда
не прекращается. В таком случае мы будем иметь совершенный частотный анализ,
причем запись спектра сигнала будет произведена идеальным записывающим
устройством. Мы можем также допустить, что вязкость жидкости, которая создает
трение и в которую погружены резонаторы, настолько велика, что величиной
колебаний можно фактически пренебречь. Все резонаторы будут вести себя
совершенно одинаково: каждый будет колебаться только во время действия сигнала,
после чего колебание затухнет со скоростью, пропорциональной приложенной силе.
Данное устройство позволит иметь прекрасный анализ времени - оно
"запишет" входную волну.
Следовательно, должно
быть ясно, что любой заданной волне может соответствовать не одно изображение в
координатах интенсивность - частота - время, а бесконечно большое количество
изображений. Между методом чистого временного анализа и чистого частотного
анализа может быть любой компромиссный метод по нашему желанию. Хотя слуховая
система человека не является столь простой, как ряд настроенных контуров, но и
здесь можно использовать компромисс. Суть его, заключающаяся в решении проблемы
отношения частоты и времени, является одной из центральных проблем в области
психологии слуха */Данная проблема может быть выражена путем противопоставления
колебания и его функции автокорреляции вместо противопоставления колебания и
спектра. Компромиссное решение представляет в таком случае "текущую"
функцию автокорреляции. Фэно и Хаггнис сделали предположение, что слуховой
механизм легче понять как автокоррелятор, чем как анализатор частоты/.
Хотя при предыдущем
анализе мы на одной и той же картине имели как время, так и частоту, это далось
нам дорогой ценой. Дело в том, что, когда мы добивались точности в определении
одного, мы в известном смысле утрачивали эту точность в определении другого.
Часто проводится аналогия между изучаемой в настоящее время проблемой время -
частота и проблемами момент - положение и энергия - время, которые привели
Гайзенберга (1927) к утверждению его принципа неопределенности.
Формально аналогия
очень близкая.
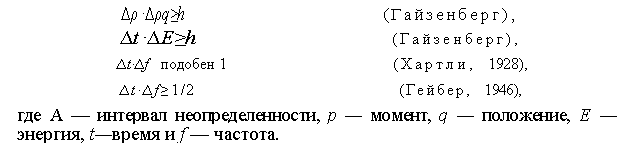
Данная аналогия
позволила Гейберу предположить, что можно найти решение проблемы время -
частота в квантовой механике, а Джусу (1948) говорить о наличии "темного
пятна" (района неопределенности) в изображениях акустических колебаний в
координатах интенсивность - частота - время. Однако следует заметить, что в
отношении спектра, соответствующего определенному колебанию, никакой
неопределенности нет независимо от длительности колебания.
Единственно, в чем
можно усмотреть неопределенность относительно частоты колебания малой
длительности, так это в том, что в таком колебании много частотных
составляющих. И наоборот, узкополосный спектр предполагает растянутые волны;
волна, соответствующая данному узкополосному спектру, может быть определена
совершенно точно.
Звуковая
интенсивность и децибелы
Интенсивность звуковой
волны, как мы видели, обычно измеряется прибором для измерения давления в
единицах давления, то есть в динах на 1 кв.см. Иногда, однако, более удобно
определять интенсивность звука в единицах мощности или энергии */В физической
акустике термин "интенсивность" всегда обозначает мощность или
энергию, или точнее, плотность потока энергии. В данной главе мы считаем удобным
применять слово "интенсивный" в качестве общего термина по отношению
к амплитуде, давлению, напряжению, мощности, энергии и т. п./. Зависимость
между давлением плоской волны в свободном поле и акустической мощностью проста,
поскольку воздух представляет собой почти полностью упругую среду.
В упругой среде так
называемая объемная скорость u всегда прямо пропорциональна давлению a.
Поскольку мощность P равна давлению, умноженному на объемную скорость, мы имеем
следующие отношения:
![]()
где с - величина, обратная акустическому сопротивлению воздуха. Из третьего
уравнения видно, что мощность пропорциональна квадрату давления. Шкала децибел
представляет собой в основном логарифмическую форму шкалы мощности или энергии.
Для того чтобы получить более удобные величины единиц, бел (логарифмическая
единица) делится на 10 дб. Отсюда число децибелов, соответствующее заданному
отношению акустической мощности или энергии, составит
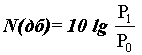
Таким образом, если
одна звуковая интенсивность Р1, измеряемая в единицах мощности или энергии, в
10 раз больше другой звуковой интенсивности Р0, измеряемой в тех же единицах,
то Р1 будет на 10 дб больше Р0. Следует учесть, что величина "10 дб"
представляет собой отношение интенсивностей, а не абсолютную интенсивность.
Чтобы определить абсолютную интенсивность звука в децибельной записи,
необходимо оговорить, что интенсивность звука Рe представляет собой N децибел
выше или ниже данной исходной интенсивности Р0.
Наиболее часто
применяемые исходные интенсивности равняются 1 и 0,0002 дин/кв.см. Эти величины
даны, однако, в единицах давления, а шкала децибел, как мы видели, представляет
собой в основном логарифмическую шкалу мощности. Мы можем, конечно, обойти
трудность, переведя единицы давления исходной интенсивности в единицы мощности;
можно, например, записать, что 0,0002 дин/кв.см равняются 10**16 вт/кв.см на
открытом воздухе. Более удобно, однако, принять запись в децибелах, поскольку
она выражает как отношение давления, так и отношение мощности. Если учесть, что
в сопротивляющейся среде Р = ca**2, где Р - мощность, a - амплитуда (давление),
а с - величина постоянная, то мы получим следующую формулу:
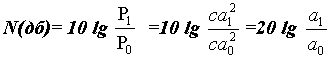
Следовательно, мы
видим, что поскольку десятикратное увеличение давления (амплитуда)
соответствует стократному увеличению мощности, оно равно +20 дб.
|
Отношение
амплитуды |
Отношение
мощности |
Децибелы |
Децибелы |
Отношение
амплитуды |
Отношение
мощности |
|
1,00 |
1,00 |
0 |
0 |
1,00 |
1,00 |
|
0,89 |
0,79 |
-1 |
+1 |
1,12 |
1,26 |
|
0,79 |
0,63 |
-2 |
+2 |
1,26 |
1,59 |
|
0,71 |
0,50 |
-3 |
+3 |
1,41 |
2,00 |
|
0,50 |
0,25 |
-6 |
+6 |
2,00 |
3,98 |
|
0,32 |
0,10 |
-10 |
+ 10 |
3,16 |
10,00 |
|
0,10 |
0,01 |
-20 |
+20 |
10,00 |
100,00 |
Другие эквиваленты
децибел для мощности и коэффициентов амплитуд представлены в приведенной выше
таблице. (О записи в децибелах см. Ра о, 1944.)